a darpa é a agência americana encarregada, há 50 anos, de pensar o futuro e criar as tecnologias que os [militares] americanos precisam. ou acham que vão precisar. e que, em alguns casos, se transformam em utilidade para todo o mundo. duas? a internet e GPS. próxima da lista? veículos completamente autônomos em tráfego urbano, talvez.
a darpa é a agência americana encarregada, há 50 anos, de pensar o futuro e criar as tecnologias que os [militares] americanos precisam. ou acham que vão precisar. e que, em alguns casos, se transformam em utilidade para todo o mundo. duas? a internet e GPS. próxima da lista? veículos completamente autônomos em tráfego urbano, talvez.
como tem que pensar no longo prazo [coisa que falta, quase sempre, à periferia], vez por outra os problemas que trata parecem não fazer nenhum sentido. muito menos quando se pensa na prática, no mundo real. mas talvez a gente deva lembrar que a internet, cujos fundamentos são dos anos 60, não fazia o menor sentido lá na partida. e não conseguiríamos mais viver sem ela, hoje.
certamente inspirada em uma das mais famosas listas de problemas de matemática de todos os tempos, enunciada por david hilbert em 1900, a darpa lançou uma relação do que considera os grandes problemas para os quais a matemática [e computação, e ciência] deveria encontrar uma solução daqui pra frente. os "novos" problemas são 23, o mesmo número de hilbert, e por sinal o dia, num janeiro de 1862, em que nasceu o grande matemático alemão. matemática cabalística, talvez, ou um búzio virtual para atrair boa sorte pra nova busca.
o primeiro problema da lista não é trivial: develop a mathematical theory to build a functional model of the brain that is  mathematically consistent and predictive rather than merely biologically inspired. ou seja: desenvolver uma teoria matemática que leve à construção de um modelo do cérebro [humano] que seja matematicamente consistente e preditivo, ao invés de meramente inspirado em biologia. pode esperar um monte de ação ao redor deste tema, até porque "investigar", para a darpa, significa "investir". e, normalmente, muito.
mathematically consistent and predictive rather than merely biologically inspired. ou seja: desenvolver uma teoria matemática que leve à construção de um modelo do cérebro [humano] que seja matematicamente consistente e preditivo, ao invés de meramente inspirado em biologia. pode esperar um monte de ação ao redor deste tema, até porque "investigar", para a darpa, significa "investir". e, normalmente, muito.
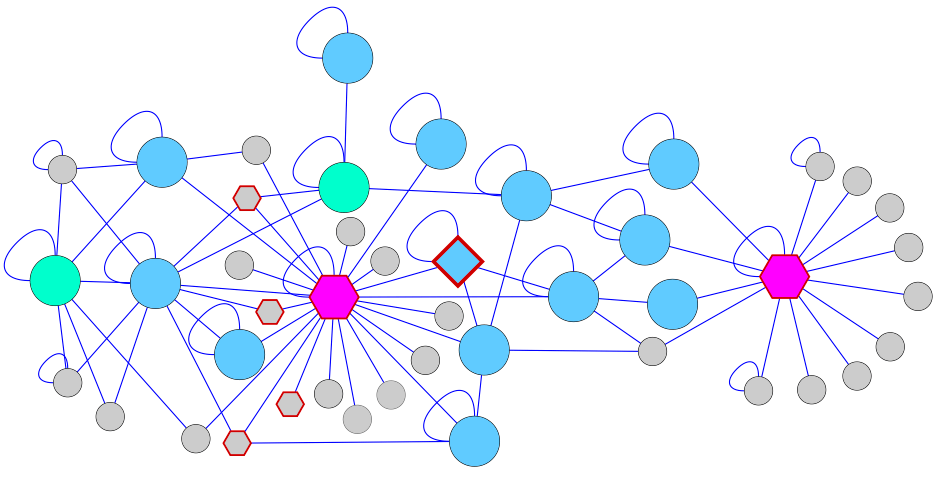
o segundo problema não é menos complexo… develop the high-dimensional mathematics needed to accurately model and predict behavior in large-scale distributed networks that evolve over time occurring in communication, biology and the social sciences. ou desenvolver a matemática de alta ordem necessária para modelar e prever o comportamento de redes distribuidas que evoluem com o tempo e que ocorrem, naturalmente, em comunicação, biologia e ciências sociais.
desafios como estes, propostos pela darpa e por hilbert, são fundamentais para o avanço da ciência. lá atrás, kurt gödel mostrou que o segundo problema de hilbert [é possível provar a consistência dos axiomas da lógica?] tem resposta negativa, ou seja, que qualquer sistema lógico minimamente interessante não pode ser provado consistente, e muito menos provado consistente dentro do próprio sistema. e isso foi o fim do sonho de hilbert de criar uma matemática completa e consistente.
o primeiro problema da darpa, se resolvido a contento, nos daria a possibilidade de… escrever cérebros, pelo menos em tese. dado um modelo "matemático", ou formal, do funcionamento do cérebro, poderíamos escrever um simulador de tal modelo teórico em software [ou o próprio modelo poderia ser descrito, de forma razoavelmente abstrata, em software] e ter, a nosso serviço, cérebros abstratos. possibilidades incríveis se abririam a partir daí. basta pensar um pouco, usando o seu… cérebro concreto.
o problema é que, lá no enunciado, está a mesma palavrinha chata usada por hilbert há cento e tantos anos: consistência. talvez, de novo, não dê pra chegar lá. mas mesmo assim vamos tentar. alguma coisa vamos conseguir, talvez mostrar que o cérebro não é passível de uma descrição matemática consistente. o que já terá sido, se ocorrer, um grande resultado.